
차원축소 목표를 위해 개발된 분석 방법
변수 간의 관계를 이해하는 것이 합리적으로 가능하지 않을 정도로 변수가 많은 경우 이것을 차원 축소를 한다. 이름에서 추측 가능하듯이 데이터 집합 내의 특징 수를 줄이기 위해 다양한 기법을 사용하는 것이다.
1. 주성분분석**
2. 요인분석(Factor Analysis)
3. 판별분석(Discriminant Analysis)
4. 군집분석(Cluster Analysis)
5. 정준상관분석(Canonical Correlation analysis)
6. 다차원척도법(Multi-dimensional scaling)
차원축소를 위해 개발된 6가지 중에 주성분 분석에 대해서 알아본다.
주성분 분석 (PCA, Pricipal Component Analysis)
- 데이터를 분석할 때 변수의 개수가 많다고 모두 활용하는 것이 꼭 좋은 것은 아님
- 오히려 변수가 '다중공선성?'이 있을 경우 분석 결과에 영향을 줄 수 있다.
(다중공선성: 설명변수 간 상관관계가 클 때를 의미한다.)
- 공분산행렬 또는 상관계수 행렬을 사용해 모든 변수들을 가장 잘 설명하는 주성분을 찾는 방법이다.
- 상관관계가 있는 변수들을 선형 결합에 의해 서로 상관관계가 없는 새로운 변수(주성분)를 만들고 분산을 극대화하는 변수로 축약한다.
 주성분 분석은 새로운 형상을 만들고 중요도가 낮은 형상을 삭제하는 방식으로 변수를 그룹화하는 형상 추출 방법이다.
주성분 분석은 새로운 형상을 만들고 중요도가 낮은 형상을 삭제하는 방식으로 변수를 그룹화하는 형상 추출 방법이다.
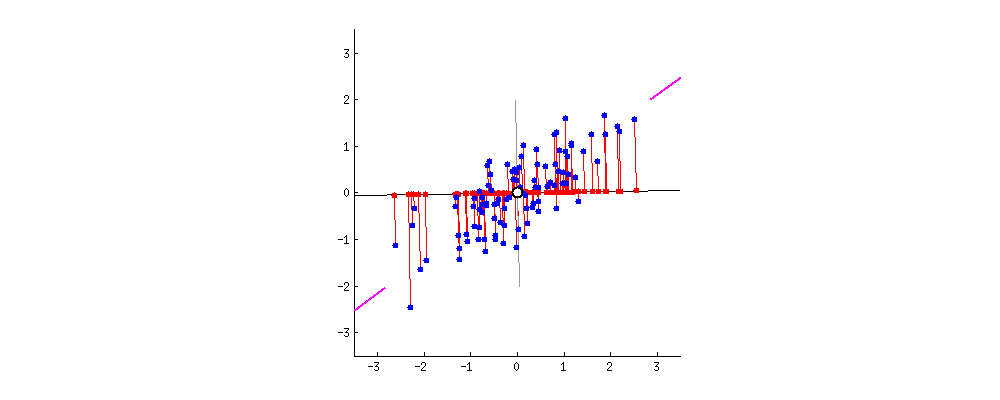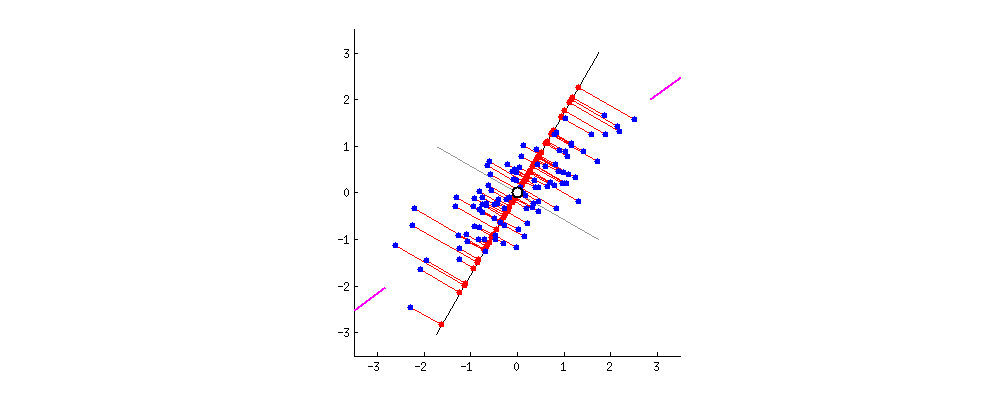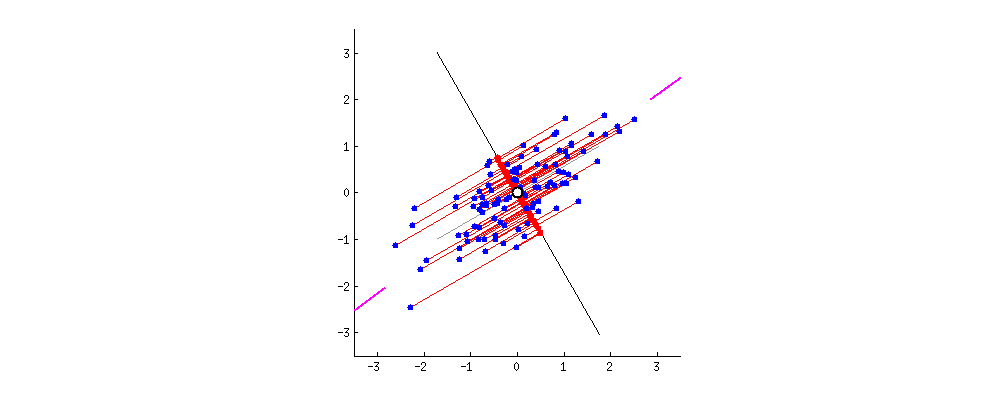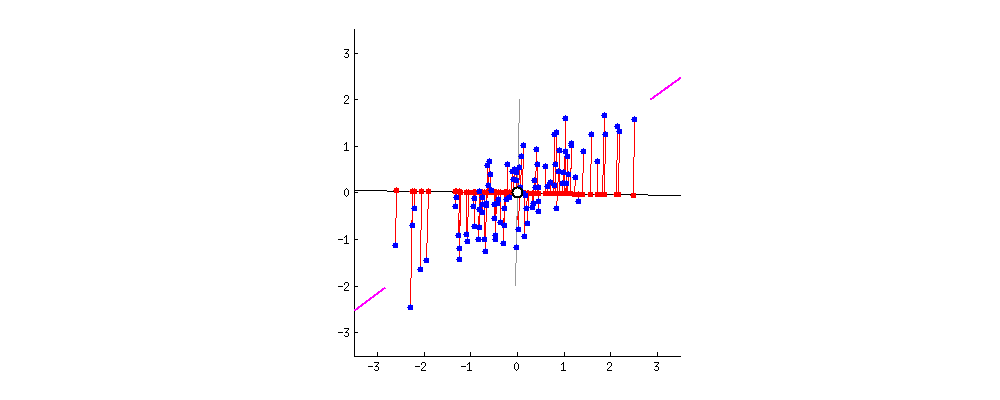 빨간색 점은 분산을 의미한다. 분산의 길이가 회전하면서 달라지는지를 관찰해본다.
빨간색 점은 분산을 의미한다. 분산의 길이가 회전하면서 달라지는지를 관찰해본다.
PCA 방법은 데이터 내에서 각 축(변수)을 따라 평균을 구한 다음 평균의 중심이 원점에 위치할 때까지 점을 이동시킨다.
주성분 분석 할 때 고민해야 하는것
Q 공분산행렬과 상관계수행렬 중 어떤 것을 선택할 것인가?
Q 주성분의 개수를 몇 개로 할 것인가?
Q 주성분에 영향을 미치는 변수로 어떤 변수를 선택할 것인가?
공분산 행렬(defualt) VS 상관계수 행렬
공분산 행렬은 변수의 측정단위를 그대로 반영한 것이고 ,상관계수 행렬은 모든 변수의 측정단위를 표준화한 것이다.
공분산행렬을 이용한 경우 측정 단위를 그대로 반영하였기 때문에 변수들의 측정 단위에 민감하다.
주성분 분석은 거리를 사용하기 때문에 척도에 영향을 받는다.(정규화 전후의 결과가 다르다.)
설문조사처럼 모든 변수들이 같은 수준으로 점수화된 경우 공분산행렬을 사용한다.
변수들의 scale이 서로 많이 다른 경우에는 상관계수행렬(correlation matrix)을 사용한다.
주성분 분석 명령어
prcomp(data,scale=TRUE)
princomp(data,cor=TRUE)
주성분 결정 기준
1) 성분들이 설명하는 분산의 비율
- 누적 분산 비율을 확인하면 주성분들이 설명하는 전체 분산 양을 알 수 있음
- 누적 분산 비율이 70~90%사이가 되는 주성분 개수 선택
fit <-prcomp(USArrests, scale=TRUE)
summary(fit)
2) 고유값(Eigenvalue)
분산의 크기를 나타내며, 고윳값이 1보다 큰 주성분만 사용함
Scree plot을 활용하여 고유값이 수평을 유지하기 전단계로 주성분의 수를 선택한다.
Scree Plot 고유값을 가장 큰 값에서 가장 작은 값을 순서로 정렬해 보여줌(1보다 큰 값 사용)
주성분 분석(PCA)해석
Standard deviation(표준편차): 자료의 산포도를 나타내는 수치로, 분산의 양의 제곱근, 표준편차가 작을수록 평균값에서 변량들의 거리가 가깝다.
Proportion of Variance(분산비율): 각 분산이 전체 분산에서 차지하는 비중, 각 자료들의 분산비율을 합치면 누적비율이 된다.
Cumulative Proportion(누적비율): 분산의 누적 비율 주성분 분석에서 누적기여율이 85% 이상이면 주성분의 수로 결정할 수 있다.
importance of components:
PC1 PC2 PC3 PC4 PC5
Standard deviation (표준편차) 1.6618 1.2671 0.7420 0.25311 0.13512
Proportion fo Variance(분산비율) 0.5523 0.3211 0.1101 0.01281 0.00365
Cumulative Proportion(누적비율) 0.5523 0.8734 0.9835 0.99635 1.0000
위에서 누적 비율 0.8734까지 주성분의 수로 정하면 주성분은 2개가 된다.